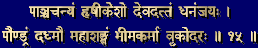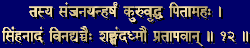Why I'm not playing T2
- Thread starter Natural
- Start date
Error|550 said:
Wow, i sense some post-IE pride outta you.
The league was only competative after IE left because IE dominated all of those teams. The came back outta retirement @ Gala and won...
IE was one of the first teams to find working strats, many teams copied them afterwards
CF *huggle*]CkB[DiamondSoul
Veteran X
There are at least two kinds of paradoxes. Propositions that logically contradict themselves (such as the proposition that “Pencils are not pencils”) may be called logical paradoxes. Propositions that logically contradict being known by us (such as the proposition that “It is raining, but we don’t believe it”) may be called pragmatic paradoxes[2]. Note that logical paradoxes are paradoxical to everyone, but (some) pragmatic paradoxes are only paradoxical to certain people. For example, the proposition “It’s raining, but I don’t believe it” is paradoxical to me, but not to you. It would be paradoxical for me to know it, for to do so would require that I both believe and disbelieve that “It’s raining”. However, nothing about this proposition would make it especially paradoxical for you to know it, if it were true.
Does the relativism of pragmatic paradoxes mean that we should treat them any differently from logical ones? Not much. We should, of course, label the paradoxes differently, but any reasons for disbelieving logical paradoxes are also be reasons for us to disbelieve any propositions that happen to be pragmatically paradoxical for us. The avoidance of logical paradoxes is built-in to most systems of logic. Kant deserved some credit for realizing that avoidance of pragmatic paradoxes should figure into such systems as well. In sections three and four, I will suggest how this might be done.
Propositions that are paradoxical all by themselves are oddities that most people encounter only rarely. More often, we deal with paradoxes that arise from combinations of beliefs. For example, suppose Jason thought that his daughter, Mandy, was in school, but then saw her playing in a neighbor’s yard (which is not in school). Neither the proposition “Mandy is in school”, nor the proposition “Mandy is in the neighbor’s yard (which is not in school)” is paradoxical by itself, but they are logically paradoxical in combination. Thus, when Jason sees Mandy in the neighbor’s yard, he may feel obliged to reevaluate his beliefs—Are his eyes deceiving him? Or was he wrong to think that Mandy was in school? In such situations, recognition of paradoxes can be extremely useful. It is only because Jason has a policy of disbelieving paradoxes that he can utilize his observation to recognize Mandy’s truancy. Similarly, even if he held no previous belief regarding the whereabouts of his dog, Sam, Jason’s policy of avoiding paradoxes would allow him use an observation of Sam in a neighbor’s yard to decide that Sam also is not in school (nor in the house). Here Jason takes advantage of the potential for paradox in the combination of his beliefs.
The paradoxes that arise in combinations of beliefs are not only most often useful—they are also the most likely to go unnoticed. Propositions can combine in complex ways to yield implications. It has taken mathematicians hundreds of years to figure out how certain propositions are implied by certain small sets of axioms. Compared to such sets of axioms, our personal sets of beliefs are tremendously numerous. Imagine, then, how much more difficult it would be to identify all of the paradoxes and potential paradoxes in a typical person’s full set of beliefs! The grand prospects for unrecognized paradoxes and potential paradoxes make it plausible that a great deal of belief modification could result from mere reflection on our current beliefs, independent of gathering new observations. Let’s call this activity of seeking paradoxes and potential paradoxes in our beliefs “paradox testing”.
What is the status of “paradox testing” relative to empirical testing? In his Republic, Plato used his famous allegory of the Sun, Line and Cave to describe the path to knowledge as consisting of four consecutive stages. The first stage is that of holding beliefs. The second is that of knowing what those beliefs are. The third is that of knowing that they do not contradict each other (i.e. the result of paradox testing). The fourth is complete knowledge of the truth. By this account, paradox testing comes before the test of truth. In other words, non-paradoxical false beliefs may pass to the third stage, but paradoxical true beliefs (if there are any) can only pass to the second. Thus, if the truth were paradoxical, then those who follow Plato would sooner choose to believe a non-paradoxical fantasy than the actual (paradoxical) truth.
Of course, Plato probably expected truth to be non-paradoxical (as most of us do), in which case he did not see himself as making a choice between true vs. non-paradoxical belief. Rather, I suspect he intended to advocate a path that would lead to beliefs that were both true and non-paradoxical simultaneously. Nevertheless, it is telling that Plato’s method employs paradox testing prior to any other, including empirical testing. Perhaps this was because Plato trusted his sense of logic more than he trusted any of his other senses.
Modern scientists have also been known to set paradox testing above empirical testing. For example, when observing a magic show, a scientist may observe what appears to be a direct violation of physical laws. If he/she took empirical evidence as the highest authority in guiding his/her choice of what to believe in such situations, then he/she would believe that physical laws had changed, that the previous experiments confirming the old laws had now become obsolete. But we do not expect many scientists to react this way. Even when the subject matter is not a magic show, even when it is an experiment in their own controlled laboratories, we expect scientists to treat unexpected observations with suspicion until working out a comprehensive non-paradoxical body of theory to explain them.
Although paradox testing may have limited applicability regarding selection of beliefs about the external world, scientists treat it as the ultimate authority so far as its scope extends. Each scientist may hold a broader variety of beliefs privately, but, in their professional circles, paradoxical claims are strictly taboo. Scientists will not entertain paradoxical propositions at scientific symposiums, nor teach them in science courses, nor publish them in scientific journals. Paradox testing is so sacred an institution of science, that certain scientists in most every scientific field have devoted themselves primarily to its application. These scientists are called “theorists”, and some of the most highly respected scientists have been counted among their ranks.
Does the relativism of pragmatic paradoxes mean that we should treat them any differently from logical ones? Not much. We should, of course, label the paradoxes differently, but any reasons for disbelieving logical paradoxes are also be reasons for us to disbelieve any propositions that happen to be pragmatically paradoxical for us. The avoidance of logical paradoxes is built-in to most systems of logic. Kant deserved some credit for realizing that avoidance of pragmatic paradoxes should figure into such systems as well. In sections three and four, I will suggest how this might be done.
Propositions that are paradoxical all by themselves are oddities that most people encounter only rarely. More often, we deal with paradoxes that arise from combinations of beliefs. For example, suppose Jason thought that his daughter, Mandy, was in school, but then saw her playing in a neighbor’s yard (which is not in school). Neither the proposition “Mandy is in school”, nor the proposition “Mandy is in the neighbor’s yard (which is not in school)” is paradoxical by itself, but they are logically paradoxical in combination. Thus, when Jason sees Mandy in the neighbor’s yard, he may feel obliged to reevaluate his beliefs—Are his eyes deceiving him? Or was he wrong to think that Mandy was in school? In such situations, recognition of paradoxes can be extremely useful. It is only because Jason has a policy of disbelieving paradoxes that he can utilize his observation to recognize Mandy’s truancy. Similarly, even if he held no previous belief regarding the whereabouts of his dog, Sam, Jason’s policy of avoiding paradoxes would allow him use an observation of Sam in a neighbor’s yard to decide that Sam also is not in school (nor in the house). Here Jason takes advantage of the potential for paradox in the combination of his beliefs.
The paradoxes that arise in combinations of beliefs are not only most often useful—they are also the most likely to go unnoticed. Propositions can combine in complex ways to yield implications. It has taken mathematicians hundreds of years to figure out how certain propositions are implied by certain small sets of axioms. Compared to such sets of axioms, our personal sets of beliefs are tremendously numerous. Imagine, then, how much more difficult it would be to identify all of the paradoxes and potential paradoxes in a typical person’s full set of beliefs! The grand prospects for unrecognized paradoxes and potential paradoxes make it plausible that a great deal of belief modification could result from mere reflection on our current beliefs, independent of gathering new observations. Let’s call this activity of seeking paradoxes and potential paradoxes in our beliefs “paradox testing”.
What is the status of “paradox testing” relative to empirical testing? In his Republic, Plato used his famous allegory of the Sun, Line and Cave to describe the path to knowledge as consisting of four consecutive stages. The first stage is that of holding beliefs. The second is that of knowing what those beliefs are. The third is that of knowing that they do not contradict each other (i.e. the result of paradox testing). The fourth is complete knowledge of the truth. By this account, paradox testing comes before the test of truth. In other words, non-paradoxical false beliefs may pass to the third stage, but paradoxical true beliefs (if there are any) can only pass to the second. Thus, if the truth were paradoxical, then those who follow Plato would sooner choose to believe a non-paradoxical fantasy than the actual (paradoxical) truth.
Of course, Plato probably expected truth to be non-paradoxical (as most of us do), in which case he did not see himself as making a choice between true vs. non-paradoxical belief. Rather, I suspect he intended to advocate a path that would lead to beliefs that were both true and non-paradoxical simultaneously. Nevertheless, it is telling that Plato’s method employs paradox testing prior to any other, including empirical testing. Perhaps this was because Plato trusted his sense of logic more than he trusted any of his other senses.
Modern scientists have also been known to set paradox testing above empirical testing. For example, when observing a magic show, a scientist may observe what appears to be a direct violation of physical laws. If he/she took empirical evidence as the highest authority in guiding his/her choice of what to believe in such situations, then he/she would believe that physical laws had changed, that the previous experiments confirming the old laws had now become obsolete. But we do not expect many scientists to react this way. Even when the subject matter is not a magic show, even when it is an experiment in their own controlled laboratories, we expect scientists to treat unexpected observations with suspicion until working out a comprehensive non-paradoxical body of theory to explain them.
Although paradox testing may have limited applicability regarding selection of beliefs about the external world, scientists treat it as the ultimate authority so far as its scope extends. Each scientist may hold a broader variety of beliefs privately, but, in their professional circles, paradoxical claims are strictly taboo. Scientists will not entertain paradoxical propositions at scientific symposiums, nor teach them in science courses, nor publish them in scientific journals. Paradox testing is so sacred an institution of science, that certain scientists in most every scientific field have devoted themselves primarily to its application. These scientists are called “theorists”, and some of the most highly respected scientists have been counted among their ranks.
[FTM]Tequila
Veteran X
Hi KI long time no see man 
did you see that thing about nat writing the book on LD? It made me giggle my ass off. 
As much as people are hating this thread, Im glad its here because that one quote has brought much amusement to my dull and boring existence. Thank you to whichever idiot said it.
did you see that thing about nat writing the book on LD? It made me giggle my ass off. As much as people are hating this thread, Im glad its here because that one quote has brought much amusement to my dull and boring existence. Thank you to whichever idiot said it.]CkB[DiamondSoul
Veteran X
i haven't been around here much lately...but anyhow...
i read nat's post and although i'm playin' (and somewhat enjoyin') t2...i'm in pretty much, total agreement with him...
after playin' t1 on ogl for it's entirety (almost)...and a few scrims/matches in t2...there is no comparison... yet i'm playin t2 cuz i dig playin with the fellaz on my team and this is the game we decided to play...
now dipstick -- "If TWL offered the $2000 to a T1 ladder...and not a T2 ladder...or maybe even both...Which game would you be playing?"
i'd still like to play t1...but time is an issue for me - money doesnt' really matter to me - it's playin' with my friends and people i know/like...
i'd like to play some t1 competition again...tribes is what got me into pc games...t2 just doesn't do it for me...but i get out a hell of a lot more now...haahaha
t1 developers 0wned... the new dynamix squad (t2 guys) ch0ke(d) as bad as the red s0x (do/will)...:devil:
t1 and t2 are the only games still installed on my pc(s), yet i haven't pubbed on either for quite some time...pubs = lam0r...:smokin:
i read nat's post and although i'm playin' (and somewhat enjoyin') t2...i'm in pretty much, total agreement with him...
after playin' t1 on ogl for it's entirety (almost)...and a few scrims/matches in t2...there is no comparison... yet i'm playin t2 cuz i dig playin with the fellaz on my team and this is the game we decided to play...
now dipstick -- "If TWL offered the $2000 to a T1 ladder...and not a T2 ladder...or maybe even both...Which game would you be playing?"
i'd still like to play t1...but time is an issue for me - money doesnt' really matter to me - it's playin' with my friends and people i know/like...
i'd like to play some t1 competition again...tribes is what got me into pc games...t2 just doesn't do it for me...but i get out a hell of a lot more now...haahaha
t1 developers 0wned... the new dynamix squad (t2 guys) ch0ke(d) as bad as the red s0x (do/will)...:devil:
t1 and t2 are the only games still installed on my pc(s), yet i haven't pubbed on either for quite some time...pubs = lam0r...:smokin:
]CkB[DiamondSoul
Veteran X
]CkB[DiamondSoul
Veteran X
Given the stakes at hand, technical rigor seems warranted in our arguments about which proposition are paradoxical. The formal derivations in this paper will be given “Fitch-style”[6]. Each proposition will be represented by a capital letter or by certain compositions of such letters and certain symbols. Here are five examples of propositions (separated by commas): A, B, ~A, (A®B), and (A® (~B®B)). I will represent each derivation by a vertical line with an attached horizontal stroke. The hypotheses of the derivation will be displayed to the right of the line and above the attached stroke. Propositions inferred under those hypotheses will be displayed to the right of the line and below the attached stroke. Consider, for example:
This display represents a derivation in which the propositions on lines 1 and 2 are hypotheses and it is claimed that the proposition on line 3 follows from these hypotheses. Derivations may be nested, and the vertical lines for derivations without hypotheses will have no horizontal strokes. For example:
Here we see three nested derivations. The propositions on lines 2 thru 4 form a subderivation of the derivation spanning lines 1 thru 5, which is, itself, a subderivation of that spanning 1 thru 6. Note that since the proposition on line 2 is a hypothesis, it is not said to follow from the proposition on line 1, even though it appears below it and to the right of the same vertical line (hypotheses are the only exception to this rule). The propositions on lines 3 and 4 are said to follow from the combination of the propositions on lines 1 and 2, the proposition on line 5 is said to follow from just the proposition on line 1, and the proposition on line 6 is claimed to be true in any case (no hypotheses).
Derivations are said to be “valid” if each non-hypothesis line can be justified by one of a set of agreed upon rules (in my official derivations, I will list the justifying rule for each line in a column to the right). I will now propose four rules and attempt to justify their acceptance. The first rule, called the “reiteration rule”, states that any sentence may be reiterated below it in the same derivation (i.e. so long as the vertical line on the left continues to that point). In the example immediately above, for example, line three is justified by the reiteration rule, since it is nothing more than a reiteration of line one. For a more complex example, consider the allowed scope of reiteration in the following Fitch-style display. We see one large derivation with two subderivations such that line seven could reiterate lines 1, 2, 5 or 6, but not lines 3, 4 or 8 (or anything after that):
The reiteration rule does not need any special justification regarding its applicability to propositions about the external world. The need to adopt this rule is simply a (minor) handicap of Fitch-style displays that is required to allow such displays to accurately represent what is meant by “derivations”. It does not represent a metaphysical claim. (I think the elegance of the display more than compensates for the inconvenience). The second rule, also a standard one, is the rule of “® introduction” (read “implication introduction”). I will represent implication with the symbol ‘ ® ’ such that for any two propositions, A and B, “(A®B)” will be defined to mean “There is a derivation from A to B” (which will also be the meaning of “A implies B”). The rule works as displayed below:
This display represents a derivation in which the propositions on lines 1 and 2 are hypotheses and it is claimed that the proposition on line 3 follows from these hypotheses. Derivations may be nested, and the vertical lines for derivations without hypotheses will have no horizontal strokes. For example:
Here we see three nested derivations. The propositions on lines 2 thru 4 form a subderivation of the derivation spanning lines 1 thru 5, which is, itself, a subderivation of that spanning 1 thru 6. Note that since the proposition on line 2 is a hypothesis, it is not said to follow from the proposition on line 1, even though it appears below it and to the right of the same vertical line (hypotheses are the only exception to this rule). The propositions on lines 3 and 4 are said to follow from the combination of the propositions on lines 1 and 2, the proposition on line 5 is said to follow from just the proposition on line 1, and the proposition on line 6 is claimed to be true in any case (no hypotheses).
Derivations are said to be “valid” if each non-hypothesis line can be justified by one of a set of agreed upon rules (in my official derivations, I will list the justifying rule for each line in a column to the right). I will now propose four rules and attempt to justify their acceptance. The first rule, called the “reiteration rule”, states that any sentence may be reiterated below it in the same derivation (i.e. so long as the vertical line on the left continues to that point). In the example immediately above, for example, line three is justified by the reiteration rule, since it is nothing more than a reiteration of line one. For a more complex example, consider the allowed scope of reiteration in the following Fitch-style display. We see one large derivation with two subderivations such that line seven could reiterate lines 1, 2, 5 or 6, but not lines 3, 4 or 8 (or anything after that):
The reiteration rule does not need any special justification regarding its applicability to propositions about the external world. The need to adopt this rule is simply a (minor) handicap of Fitch-style displays that is required to allow such displays to accurately represent what is meant by “derivations”. It does not represent a metaphysical claim. (I think the elegance of the display more than compensates for the inconvenience). The second rule, also a standard one, is the rule of “® introduction” (read “implication introduction”). I will represent implication with the symbol ‘ ® ’ such that for any two propositions, A and B, “(A®B)” will be defined to mean “There is a derivation from A to B” (which will also be the meaning of “A implies B”). The rule works as displayed below:
[FTM]Tequila
Veteran X
Thank you Cavalier, your "Natural wrote the book on LD" comment brought many giggles my way.